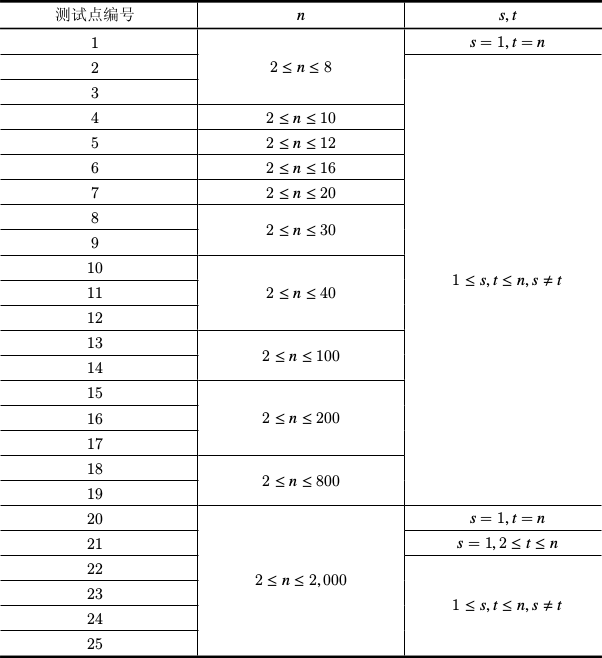
YZOJ P3669 [USACO2008 Mar]土地购买
时间限制:1000MS 内存限制:262144KB
难度:\(6.0\) (自评)
-
题目描述
农夫 John 准备扩大他的农场,他正在考虑 \(N\) (\(1 \leq N \leq 1,000,000\)) 块长方形的土地。
每块土地的长宽满足 (\(1 \leq\) 宽 \(\leq 1,000,000\), \(1 \leq\) 长 \(\leq 1,000,000\))。每块土地的价格是它的面积,但 FJ 可以同时购买多块土地。
这些土地的价格是它们最大的长乘以它们最大的宽,但是土地的长宽不能交换。如果 FJ 买一块 \(3 \times 5\) 的地和一块 \(5 \times 3\) 的地,则他需要付 \(5 \times 5=25\)。
FJ 希望买下所有的土地,但是他发现分组来买这些土地可以节省经费。他需要你帮助他求出最小的经费。
-
输入格式
输入文件的第 \(1\) 行一个数 \(N\), 表示土地块数。第 \(2\) 行至第 \(N+1\) 行,每行包含两个数,表示第 \(i\) 块土地的长和宽。
-
输出格式
最小的可行费用。
-
样例输入
|
1 2 3 4 5 |
4 100 1 15 15 20 5 1 100 |
-
样例输出
|
1 |
500 |