YZOJ P3782 [校内训练20180619]组合数问题

时间限制：1000MS 内存限制：524288KB

难度：$6.5$ 出题人：zzx

• 题目描述

• 输入格式

第一行一个正整数 $n$ 表示数对个数。

接下来 $n$ 行，第 $i$ 行两个正整数 $a_i, b_i$，表示一个数对 $(a_i, b_i)$ 。

• 输出格式

一行一个整数，表示所求式子的值。

• 样例输入

• 样例输出

• 样例说明

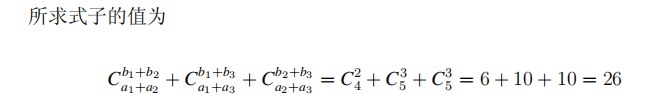
• 数据规模与约定

保证 $2 \leq n \leq 200,000$ ， $1 \leq b_i \leq a_i \leq 2000$ 。

 

 

 

---

 

 

 

首先可以得到 $\sum\limits_{i = 1}^n {\sum\limits_{j = i + 1}^n {\mbox{C}_{{a_i} + {a_j}}^{{b_i} + {b_j}} = \frac{1}{2}\left( {\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\mbox{C}_{{a_i} + {a_j}}^{{b_i} + {b_j}}} } – \sum\limits_{i = 1}^n {\mbox{C}_{2{a_i}}^{2{b_i}}} } \right)} }$ 。

只需要快速求出 $\sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\mbox{C}_{{a_i} + {a_j}}^{{b_i} + {b_j}}} }$ 。

发现 $\left( {\begin{array}{*{20}{c}} {0,}&0 \end{array}} \right) – \left( {\begin{array}{*{20}{c}} {n,}&m \end{array}} \right) = \mbox{C}_{n + m}^m$ （注：$\left( {\begin{array}{*{20}{c}} {0,}&0 \end{array}} \right) – \left( {\begin{array}{*{20}{c}} {n,}&m \end{array}} \right)$ 为从 $\left( {\begin{array}{*{20}{c}} {0,}&0 \end{array}} \right)$ 至 $\left( {\begin{array}{*{20}{c}} {n,}&m \end{array}} \right)$ 向上或向右走的路径总条数），因为总共走了 $n+m$ 个单位长度，其中分别 $n$ 个单位长度向右走且 $m$ 个单位长度向上走（$\mbox{C}_{n+m}^m=\mbox{C}_{n+m}^n$）。

所以 $\begin{array}{c} \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^n {\mbox{C}_{{a_i} + {a_j}}^{{b_i} + {b_j}}} } = \left( {\begin{array}{*{20}{c}} {0,}&0 \end{array}} \right) – \left( {\begin{array}{*{20}{c}} {{a_i} + {a_j} – {b_i} – {b_j},}&{{b_i} + {b_j}} \end{array}} \right)\\ = \left( {\begin{array}{*{20}{c}} { – {a_j} + {b_j},}&{ – {b_j}} \end{array}} \right) ~- \left( {\begin{array}{*{20}{c}} {{a_i} – {b_i},}&{{b_i}} \end{array}} \right) \end{array}$ 。

即求所有 $\left( {\begin{array}{*{20}{c}} { – {a_j} + {b_j},}&{ – {b_j}} \end{array}} \right)$ 至所有 $\left( {\begin{array}{*{20}{c}} {{a_i} – {b_i},}&{{b_i}} \end{array}} \right)$ 的路径总条数，因为左边右边分别只与 $i, j$ 有关，所以简单DP即可。

设 $f_{i, j}$ 为从右上角所有出发点向左下方走到 $(i, j)$ 时的路径总条数。显然，当前 $\left( {\begin{array}{*{20}{c}} {i,}&{j} \end{array}} \right)$ 等于某个 $\left( {\begin{array}{*{20}{c}} {{a_k} – {b_k},}&{{b_k}} \end{array}} \right)$ 时，那么路径条数要 $+1$ ，否则不用，即 $f_{i, j}=f_{i+1, j}+f_{i, j+1}+mpos\left( {\begin{array}{*{20}{c}} {i,}&{j} \end{array}} \right)$ ， $mpos\left( {\begin{array}{*{20}{c}} {x,}&{y} \end{array}} \right)$ 表示有几个 $\left( {\begin{array}{*{20}{c}} {{a_k} – {b_k},}&{{b_k}} \end{array}} \right)$ 等于 $\left( {\begin{array}{*{20}{c}} {x,}&{y} \end{array}} \right)$ （相当于DP的初始值）。当遇到 $\left( {\begin{array}{*{20}{c}} { – {a_k} + {b_k},}&{ – {b_k}} \end{array}} \right)$ 时直接贡献答案即可。

最后别忘了减去 ${\sum\limits_{i = 1}^n {\mbox{C}_{2{a_i}}^{2{b_i}}} }$ ，除以 $2$ 其实并不需要逆元。

因为坐标有的为负，记得数组下标整体偏移。