时间限制：1000MS 内存限制：131072KB
难度：\(5.0\)
一共有 \(N\) 种数字，所以按照包含数字的集合分类，可能有 \(2^N\) 类不同的集合。每个集合包含一种特定的数字的概率都是 \(\displaystyle\frac{1}{2}\) 。
随机取其中 \(k\) 个集合，请你帮忙算一下其中存在两个集合完全相同的概率。
一行两个整数 \(N,k\) 。
两个正整数，分别表示概率（最简分数）的分子和分母。分别对 \(10^6+3\) 取模吧。
\(1 \leq N \leq 10^{18}\)，\(2 \leq k \leq 10^{18}\) 。
时间限制：1000MS 内存限制：131072KB
出题人：chj2001 难度：\(5.4\)
存在 \(n\) 种物品，其中第 \(i\) 种物品的价值为 \(a_i\) ，最多可以用 \(b_i\) 件，求从这些物品中选取若干件（不能为 \(0\) 件），得到的总价值为 \(9\) 的倍数的方案。
需要分别计算每种物品中，每件之间有区别的方案数和没有区别的方案数。
（即每种物品按照 \(1,2,3, \cdots ,b_i\) 编号的方案数和不编号的方案数。）
第一行输入一个数 \(n\) 。
接下来 \(n\) 行，每行两个数 \(a_i, b_i\) 。
输出共两行，每行各包括一个数，分别表示对于每种物品视为不同的时的方案数和视为相同的时的方案数。有的时候方案数可能很大，你需要将它对 \(10^9+7\) 取模。
方案数均不考虑顺序，如 \(2, 3, 4\) 和 \(4, 3, 2\) 是同一种方案。
如果无法做到则输出 \(0\) 。
|
1 2 3 |
2 2 3 3 3 |
|
1 2 |
4 2 |
不考虑同种物品之间的区别，一共有 \(2\) 种不同的方案凑出 \(9\) 的倍数，即 \(3, 2, 2, 2\) 和 \(3, 3, 3\) 。
考虑同种和果子的区别时，一共有 \(C_3^1 \times C_3^3 = 3\) 种不同的方案凑出 \(3, 2, 2, 2\)，\(C_3^3=1\) 种方案凑出 \(3, 3, 3\)，因此总共有 \(4\) 种方案。
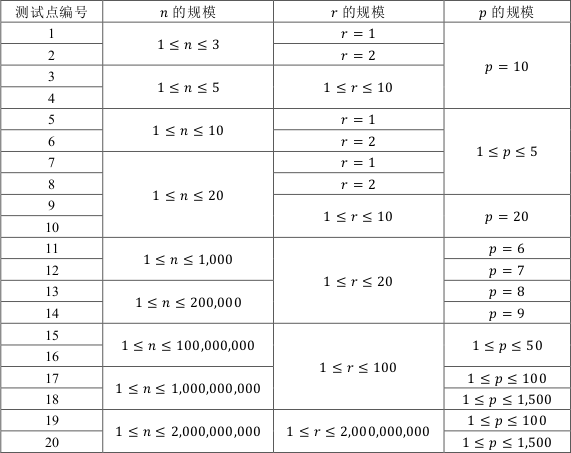
对于 \(40\%\) 的数据，\(n \le 1000 , a_i \le 100 , b_i \le 100\) 。
对于 \(100\%\) 的数据，\(1 \le n \le 10^5 , 1 \le a_i \le 90000 , 1 \le b_i \le …
时间限制：1000MS 内存限制：262144KB
难度：\(5.0\)
这里有一个关于合法的括号序列的问题。如果插入“+” 和 “1” 到一个括号序列，我们能得到一个正确的数学表达式，我们就认为这个括号序列是合法的。例如，序列 “(())()”, “()” 和 “(()(()))” 是合法的，但是 “)(“, “(()” 和 “(()))(” 是不合法的。我们有一个仅由 “(”，“)” 和 “?” 组成的括号序列，你必须将 “?” 替换成括号，从而得到一个合法的括号序列。
对于给定仅由 “(”，“)” 和 “?” 组成的括号序列，你需要将 “?” 替换成括号，得到一个合法的括号序列，同时需要使得代价之和最小。
文件有多个测试实例（\(\leq 5\)）。每个实例的第一行有 \(1\) 个正整数 \(n\)，（\(1 \leq n \leq 100000\)），表示括号序列的长度为 \(n\)。第二行是一个长度为 \(n\) 的字符串，表示输入的括号序列，字符串仅由 “(”，“)” 和 “?” 组成。接下来 \(m\) 行，\(m\) 是字符串中 “?” 的个数，每一行包含两个整数 \(a_i\) 和 \(b_i\)（\(1 \leq a_i,b_i \leq 1000000\)），\(a_i\) 是将第 \(i\) 个 “?” 替换成左括号的代价，\(b_i\) 是将第 \(i\) 个 “?” 替换成右括号的代价。文件的最后一行有一个 \(0\) 表示结束。
将计算出的每个测试实例的答案依次输出到文件中。每个测试实例第一行输出一个整数，表示最小代价和。如果不存在合法方案，输出 \(-1\)。如果存在合法方案，第二行输出替换后的括号序列。若有多种替换方案的代价之和最小，可以输出任意一种。…
时间限制：1000MS 内存限制：131072KB
难度：\(5.0\)
求一个字符串的回文子序列个数。
如果 \(p_1p_2 \cdots p_m\) 满足 \(1 \leq p_1<p_2<\cdots<p_m \leq n\)，则称 \(a_{p_1}a_{p_2}\cdots a_{p_m}\) 是序列 \(a_1a_2\cdots a_n\) 的一个子序列。
如果对于所有 \(1 \leq i \leq n\) 都满足 \(a_i=a_n-i+1\)，则 \(a\) 是一个回文串。空串也是回文串。
一个字符串
回文子序列个数 \(\mod 10^9+7\)
|
1 |
akakfft |
|
1 |
10 |
样例中所有回文子序列按照字典序如下：
“”（空串）、”a”、”aa”、”aka”、”f”、”ff”、”k”、”kak”、”kk”、”t”
对于 \(100\%\) 的数据，\(n \leq 5000\) 。
字符串中仅包含小写字母。
时间限制：1000MS 内存限制：131072KB
难度：\(5.1\)
在 \(Y\) 国有 \(N\) 座城市，并且有 \(M\) 条双向公路将这些城市连接起来，并且任意两个城市至少有一条路径可以互达。\(Y\) 国的国王去世之后，他的两个儿子 \(A\) 和 \(B\) 都想成为新的国王，但他们都想让这个国家更加安定，不会用武力解决问题。于是他们想将这个国家分成两个小国家 \(A\) 国和 \(B\) 国。现在，\(A\) 拥有 \(1\) 号城市，\(B\) 拥有 \(N\) 号城市，其他的城市还尚未确定归属哪边。
由于大家都想让国家变得更好，而某些城市的人民愿意国王的 \(A\) 儿子作为他们的领袖，而某些城市更看好 \(B\)，而为了交通的便捷，如果划分后的公路连接两个同一个国家的城市，那么更利于城市之间的交流。于是大臣们设计了一种对土地划分的评分机制，具体如下：
1，对于城市 \(i\) ，如果它划分给 \(A\) 国，将得到 \(VA[i]\) 的得分；划分给 \(B\) 国，将得到 \(VB[i]\) 的得分。
2，对于一条公路 \(i\) ，如果它连接两个 \(A\) 国的城市，将得到 \(EA[i]\) 的得分；连接两个 \(B\) 国的城市，将得到 \(EB[i]\) 的得分；否则，这条公路将失去意义，将扣除 \(EC[i]\) 的得分。
现请你找到最优的土地划分，使得这种它的评分最高。
第一行包含两个整数 \(N\)，\(M\)，含义如问题描述所示。
接下来一行 \(N-2\) 个非负整数，表示 \(VA[2..N-1]\) 。
接下来一行 \(N-2\) 个非负整数，表示 \(VB[2..N-1]\) 。
接下来 \(M\) 行，每行五个非负整数描述一条公路：\(X, Y, EA[i], EB[i], EC[i]\)，含义如问题描述所示。
输出一个整数，表示最高评分。
|
1 2 3 4 5 6 |
3 3 8 9 1 2 2 6 2 2 3 8 5 7 1 3 9 4 1 |
|
1 |
11 |
\(100\%\) 的数据 \(N \leq 10000, M \leq 40000\)；
时间限制：1000MS 内存限制：262144KB
难度：\(5.5\)
班里有 \(n\) 个同学。老师为他们选了 \(n\) 个笔名。现在要把这些笔名分配给每一个同学， 每一个同学分配到一个笔名，每一个笔名必须分配给某个同学。现在定义笔名和真名之间的相关度是他们之间的最长公共前缀。设笔名为 \(a\)，真名为 \(b\)，则他们之间的相关度为 \(lcp(a,b)\)。那么我们就可以得到匹配的质量是每一个同学笔名和真名之间相关度的和。
对于两个字符串 \(a,b\)（从 \(1\) 开始标号），定义 \(a,b\) 的最长公共前缀 \(lcp(a,b)\) 为最大的非负整数 \(k\)，使得 \(k\le |a|, k\le |b|\)，且对所有 \(i=1,2,\ldots,k\)，\(a_i = b_i\) 。
给出一种分配笔名的方案，使得匹配质量最大。
第 \(1\) 行有 \(1\) 个整数 \(n\)，表示班级中同学的数目。接下来 \(n\) 行，表示每一个同学的真名。最后 \(n\) 行是老师已经安排好的笔名。每行的名称仅由小写字母组成。
将分配笔名的方案输出到文件中。第一行输出一个数，表示最大匹配质量。接下来 \(n\) 行，每行两个数 \(a,b\)，表示把编号为 \(b\) 的笔名分配给编号为 \(a\) 的同学。同学和笔名均按输入顺序从 \(1\) 至 \(n\) 编号。若方案不唯一，任意输出一种即可。
|
1 2 3 4 5 6 7 8 9 10 11 |
5 gennady galya boris bill toshik bilbo torin gendalf smaug galadriel |
|
1 2 3 4 5 6 |
11 4 1 2 5 1 3 5 2 3 4 |
对于所有测试点，\(n \leq 100000\)，输入串总长 \(\leq 800000\) 。
时间限制：2000MS 内存限制：131072KB
难度： \(5.7\)
给定一个长度为 \(N\) 的非负整数序列 \(a\) ，现要把它分割成 \(k+1\) 个连续非空的子序列。
每次分割可以选择一段剩余长度超过 \(1\) 的序列，并在其中选择一个位置，把它分割成两个连续非空的子序列。这样做可以得到一些 \(Bonus\)，为分割出的两个新序列中元素和的乘积。
现要找到一种方案，使得经过 \(k\) 次分割后，能得到的 \(Bonus\) 最多。
第一行包含两个整数 \(n, k\) ；
第二行包含 \(n\) 个非负整数，表示序列 \(a\) 。
第一行包含一个整数，为最大 \(Bonus\) 。
第二行包含 \(k\) 个 \(1\) 到 \(n-1\) 的整数，表示最优方案。其中第 \(i\) 个数 \(x_i\) 表示在该方案中，进行第 \(i\) 次操作时，应该选择第 \(x_i\) 个数后面的位置，并将这个数所在的序列分成两部分。
如果有多个最优方案，输出其中任意一种即可。
|
1 2 |
7 3 4 1 3 4 0 2 3 |
|
1 2 |
108 1 3 5 |
数据满足 \(2 \leq n \leq 100000\)，\(1 \leq k \leq min\{n-1,200\}\) 。
时间限制：1000MS 内存限制：131072KB
难度： \(5.1\)
在初中数学课上，\(Alkri\) 学习了圆的相关知识，他对与圆有关的问题更加感兴趣了。
\(Alkri\) 想在平面直角坐标系的第一象限中依次画 \(n\) 个与两坐标轴均相切的圆，其中，第 \(1\) 个圆的半径为 \(r\)，之后的每个圆都比上一个圆大，且与上一个圆相切，也就是说，对所有整数 \(2 \leq i \leq n\)，第 \(i\) 个圆的半径大于第 \(i-1\) 个圆的半径且与第 \(i-1\)个圆相切。
例如当 \(n=3\) 时，三个圆 \(C_1, C_2, C_3\) 如下图所示（由于 \(C_3\) 比较大，未画完整）：
现在，\(Alkri\) 很好奇：第 \(n\) 个圆的半径 \(R\) 到底有多大？他知道 \(R\) 不一定是整数（真聪明！），并且可能非常大，所以只需要你保留 \(R\) 的整数部分（向下取整）的末尾 \(p\) 位数字即可。
输入仅一行，包含三个整数 \(n\)，\(r\)，\(p\)，意义如题目所述。
输出仅一行一个整数，表示第 \(n\) 个圆的半径 \(R\) 的整数部分的末尾 \(p\) 位。注意当 \(R\) 的整数部分实际位数超过 \(p\) 时需要输满 \(p\) 位（即需要保留前导0），如果实际位数不满 \(p\) 位则不用补前导 0 。
|
1 |
10 5 5 |
|
1 |
08989 |
第 \(10\) 个圆的半径整数部分为 \(38808989\)，要求输出整数部分的末尾 \(5\) 位数，因此输出 \(08989\) 。注意保留前导 0 。
时间限制：2000MS 内存限制：262144KB
难度：\(5.2\)
给定一个长度为 \(n\) 的非负整数序列 \(a\) 和一个正整数 \(m\) 。
现在有 \(q\) 组询问，每组询问给定两个正整数 \(l, r\) ，每次可以选择满足 \(l \leq i \leq r\) 的若干个 \(a_i\) （也可以一个都不选），使得这些 \(a_i\) 的和是 \(m\) 的非负整数倍，并输出满足条件的选择方案数对 \(10^9+7\) 取模后的余数。
第一行为两个正整数 \(n\) 和 \(m\) 。
第二行为序列 \(a\) ，共 \(n\) 个元素，用一个空格隔开。
第三行为询问数 \(q\) 。
接下来的 \(q\) 行，每一行都有两个正整数，分别为 \(l\) 和 \(r\) 。
共 \(q\) 行。
第 \(i\) 行为第 \(i\) 组询问的答案。
|
1 2 3 4 5 6 7 |
4 3 5 1 3 2 4 1 2 1 3 1 4 2 4 |
|
1 2 3 4 |
2 4 6 4 |
对于第一组询问 \(l=1, r=2\) ，有 不选、选择 \(5, 1\) ，共 \(2\) 种情况。
时间限制：1000MS 内存限制：131072KB
难度：\(5.0\)
第一行有两个整数 \(N\) 和 \(Q\)，表示商店有 \(N\) 个装饰品，一共有 \(Q\) 个询问。
第二行有 \(N\) 对整数，每 \(i\) 对整数 \(p_i, b_i\) 表示第 \(i\) 个装饰品的价格和好看度。
接下来 \(Q\) 行，每行两个整数 \(a, c\)，分别描述 \(Q\) 个询问。
对于每个询问输出一行，一个整数表示最大好看度。
|
1 2 3 4 5 6 7 |
3 5 2 3 1 3 1 2 1 2 1 1 3 1 3 2 3 3 |
|
1 2 3 4 5 |
5 3 3 3 6 |
对于 \(30\%\) 的数据，\(N \leq 100, Q \leq 1000\) 。
对于 \(100\%\) 的数据，\(N \leq 1000, Q \leq 100000, 1 \leq a \leq N, c \leq 1000\) 。