YZOJ P3361 [校内训练20171117]数点问题
时间限制:2000MS 内存限制:262144KB
出题人:zzx 难度:\(6.0\)
\(k\) 维空间内有两个点集 \(A=\{X_1,X_2,\ldots,X_m\}\),\(B=\{Y_1,Y_2,\ldots,Y_n\}\),每个点的坐标是一个 \(k\) 元组 \((x_1,x_2,\ldots,x_k)\)。我们称点 \(X(x_1,x_2,\ldots,x_k)\) 控制点 \(Y(y_1,y_2,\ldots,y_k)\) 当且仅当 \(\forall 1\le i\le k,x_i>y_i\),记为 \(X>Y\)。数点问题是要求计算点 \(X_i\) 能控制 \(B\) 中的点数 \(c_i\),即 \(c_i=\left| \{Y \in B\ |\ X_i > Y\} \right|\)。
对于给定的点集 \(A\) 和 \(B\),求出对于所有 \(1\le i\le m\) 的 \(c_i\) 的值。
第一行有三个正整数\(m\)、\(n\) 和 \(k\),分别表示集合 \(A\) 和 \(B\) 的基数及维数。接下来的 \(m+n\) 行依次给出点 \(X_1 , X_2 ,\ldots, X_m ,Y_1 ,Y_2 ,\ldots,Y_n\),每个点的坐标用一行 \(k\) 个整数 \(x_1 , x_2 ,\ldots, x_k\) 描述,所有坐标在 \(int\) 范围内。
将计算出的 \(c_1 ,c_2 ,\ldots,c_m\) 依次输出到文件中,每个 \(c_i\) 输出 \(1\) 行。
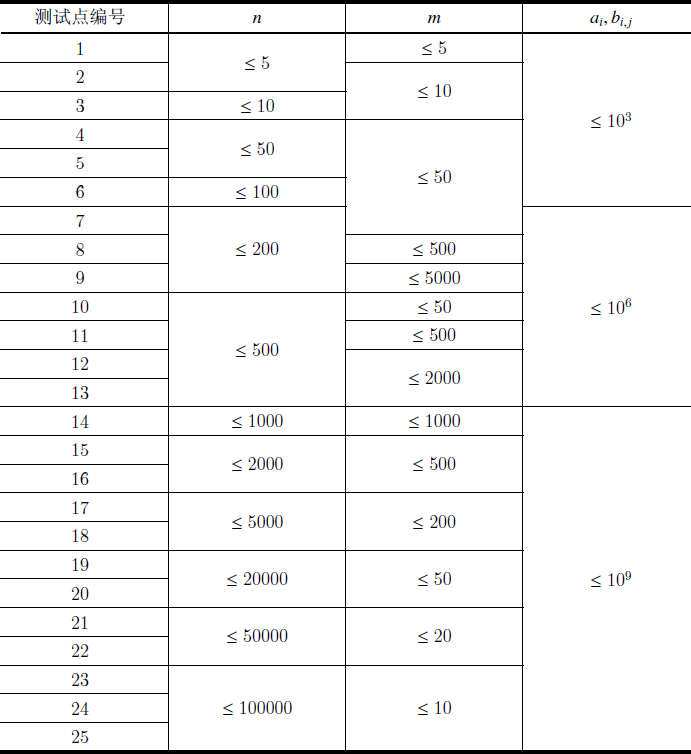
对于数据点 \(1\),\(n,m\le 200,000\),\(k=1\)…
Read the rest