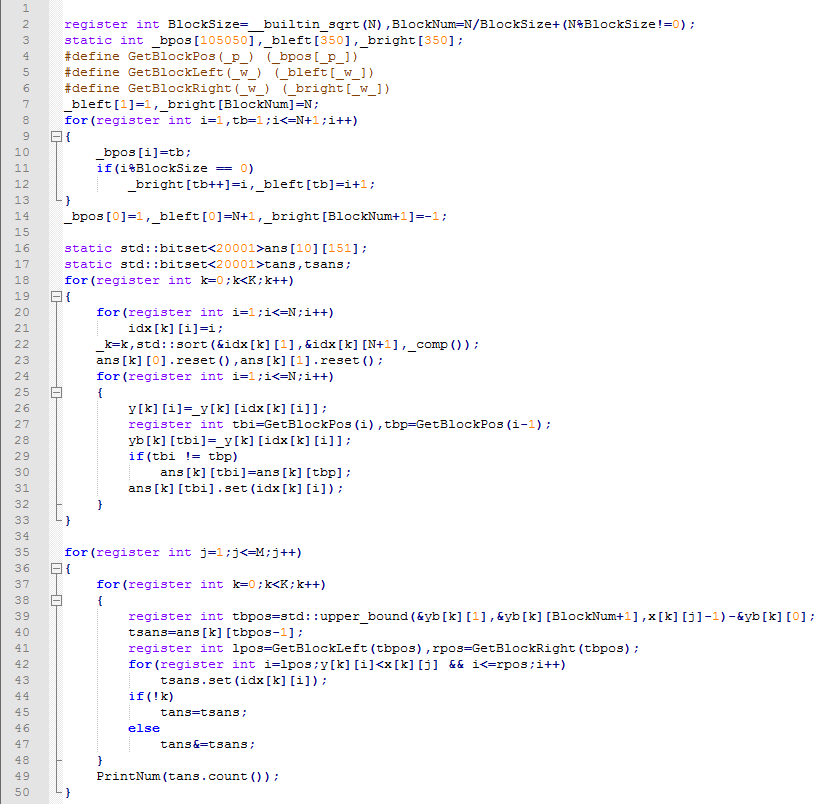
[研学] 偏序问题的研究
时间:2019.04 ~ 2019.09
参加成员:Modem_ Lagoon _Qijia mnihyc
备注:第二年就开始混水了啊(笑),只存了自己写的那部分:
-
高维偏序
至此,\(k \le 3\) 的问题已经被我们解决了。
那 \(k = 4\) 呢?CDQ套CDQ?CDQ套树套树?树套树套树?
如果 \(k\) 更大,达到 \(k = 10\) 呢?十维树状数组?树套树套树套树套………?
很明显 \(O(n{\log ^{k – 1}}n)\) 的复杂度是承受不起的,需要从别的方面下手。
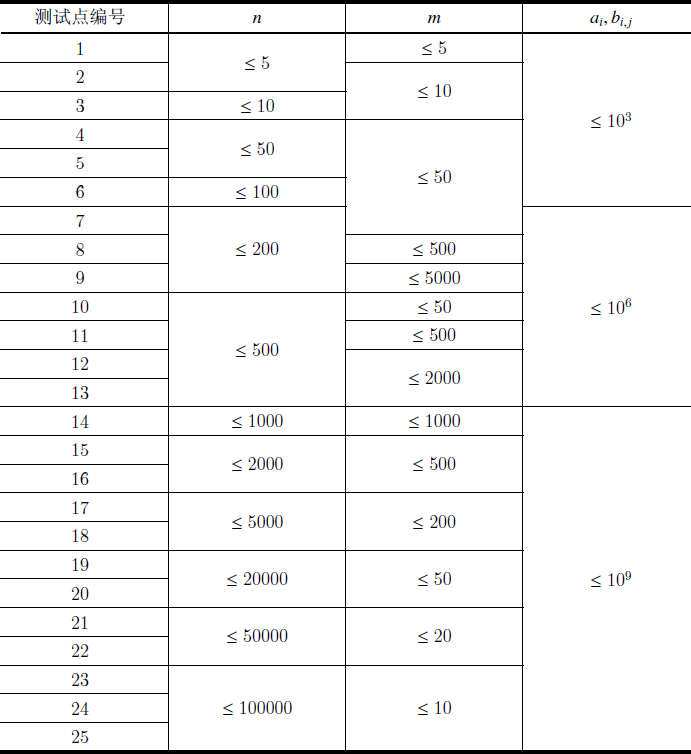
注意到在 \(k\) 变大的同时,\(n\) 也在变小,所以可以考虑复杂度以 \(n\) 为主的算法。
首先考虑的,当然是暴力啦)。
可以暴力枚举所有维度,并且按照这个维度(上的数)排序,这些就可以快速找出一个点控制了其它哪一些点。如果把这个信息用一个长度为 \(n\) 的二进制数表示,那么对于每个询问,只需要把它在所有维度下的二进制数取“与”运算(即能控制的点取交集),这样答案就是二进制位为 \(1\) 的数量了。
维护二进制串?当然是用 std::bitset<> 啦)。
这样复杂度就是 \(\displaystyle O\left( {\frac{{{n^2}k}}{{32}}} \right)\) ,足以通过本题了。
代码略。
这里其实还有一种在时空复杂度上的优化——分块)。
按照分块的那一套理论,把区间分成 \(\sqrt n \) 个,每块用一个 std::bitset<> 维护前缀,同时维护一个块最大值。查询的时候在块上二分,找到询问点所在的块,然后暴力加块内的点即可。时间复杂度即可缩小至 \(\displaystyle O\left( {\frac{{nk\sqrt n }}{{32}}} \right)\) 。