YZOJ P3840 [2018省队集训]序列
时间限制:2000MS 内存限制:524288KB
难度: \(8.0\)
-
题目描述
给定一个长度为 \(n\) 的序列 \(x\) 。
你需要从序列中选出一些位置。对于第 \(i\) 个位置,如果它被选中,你会获得 \(x_i\) 的收益;否则找到最小的 \(j\) 使得第 \(j\) 个位置到第 \(i\) 个位置都没有被选中,你需要付出 \(i-j+1\) 的代价。
此外,你选出的位置必须满足 \(x_i\) 是单调不下降的。
最大化收益减去代价的结果。
-
输入格式
第一行一个正整数 \(n\),第二行 \(n\) 个整数 \(x_1\) ~ \(x_n\) 。
-
输出格式
输出一行一个整数表示答案。
-
样例 1 输入
|
1 2 |
7 1 3 2 7 3 2 4 |
-
样例 1 输出
|
1 |
7 |
-
样例 1 说明
选择第 \(1, 3, 5, 7\) 个位置,获得收益 \(1+2+3+4=10\) ,第 \(2, 4, 6\) 个位置的代价分别为 \(1, 1, 1\) ,收益减去代价为 \(10-3=7\) 。
-
样例 2 输入
|
1 2 |
7 -3 -4 -2 -2 -6 -8 -1 |
-
样例 2 输出
|
1 |
-11 |
-
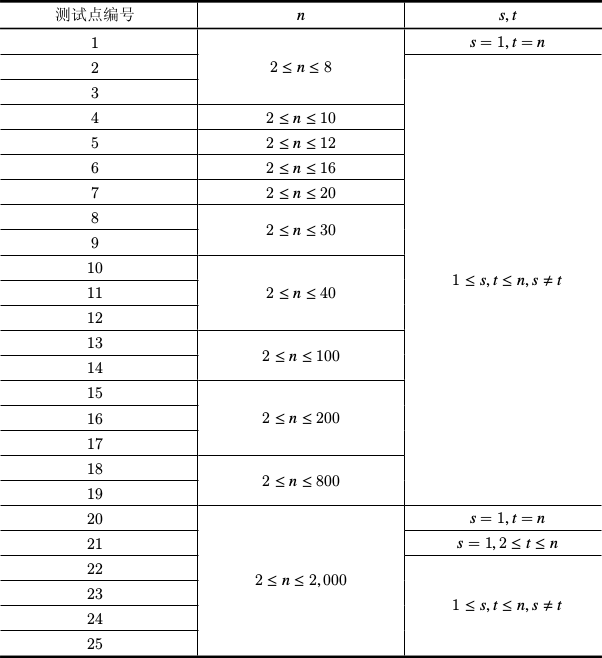
数据规模与约定