[FJWC2019 Day2] 直径

时间限制：1000MS      内存限制：524288KB

难度： $4.0$

• 题目描述

你需要构造一棵至少有两个顶点的树，树上的每条边有一个非负整数边权。树上两点 $i,j$ 的距离 $dis(i,j)$ 定义为树上连接 $i$ 和 $j$ 这两点的简单路径上的边权和。

我们定义这棵树的直径为，所有满足 $1 \leq i < j \leq n$ 的 $(i,j)$ 中，$dis(i,j)$ 最大的。如果有多个这样的 $(i,j)$，那么均为直径。

作为一个构造题，你需要构造一个恰有 $k$ 个直径的树。可以证明在给定的限制下一定有解。

• 输入格式

一行一个正整数 $k$，表示你需要构造出一个恰有 $k$ 个直径的树。

• 输出格式

第一行一个正整数 $n$，表示你构造的树的点数。

接下来 $n-1$ 行，每行三个整数 $i,j,w$，表示一条连接点 $i$ 和 $j$ （点的编号为 $1,2, \cdots, n$）的树边，边权为 $w$ 。

• 样例输入

• 样例输出

• 样例说明

这只是一种符合题意的输出，可能还有其他输出。在这个输出中，直径为 $(1,5),(3,5),(4,5)$ 。

• 数据规模与约定

注意，你需要构造出的树必须满足 $2 \leq n \leq 5000, 0 \leq w \leq 10^5$ ！

对于 $30pts$ 的数据，$1\leq k \leq 2000$ ；

对于 $100pts$ 的数据，$1\leq k \leq 5 \times 10^6$ 。

 

 

YZOJ P4260

---

 

 

 

大部分人都当场切掉了，我没有一个清醒的思路就没有构造出来。。。

首先，样例是一个菊花。可以很容易发现，要构造出 $k$ 条直径，只需要按照下图的方案：

这样就是用 $k+2$ 个点构造出一个菊花，显然有 $k$ 条最长链，拿到 $30pts$ 。

 

因为 $2 \leq n \leq 5000$ ，$k$ 很大，所以考虑将 $k$ 进行分解。我当时就想到可以往点外连 $a$ 条边权为 $1$ ， $b$ 条边权为 $2$ 形成的菊花，这样答案就是 $k=a \times b$ ，可以把 $k$ 变小。但是这样做的话万一 $k$ 是个大质数，那又完蛋了，没有办法分解。

然而到这里我就想不下去了。其实离正解只差一步之遥：$k$ 分解的还不够。

考虑向外连三个菊花（如下图），这样 $k=ab+ac+bc$ 。

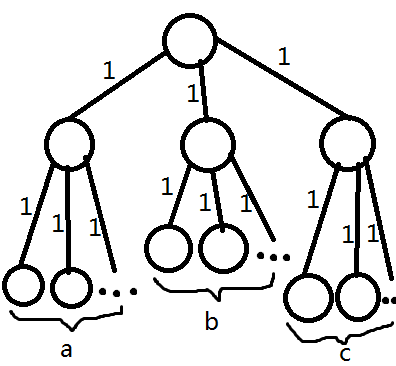
这样子就有办法分解了！

$k=ab+ac+bc=a(b+c)+bc$ ，即 $a=\frac{k-bc}{b+c}$ 。由于 $a+b+c \leq n-4$ ，所以可以直接暴力枚举 $b, c$ 然后算出合法的 $a$ ，这样就得到了一组合法的构造方案了，时间复杂度 $O(n^2)$ 。

此外，本题还可以利用边权为 $0$ 的性质挂链，或者其他一些奇奇怪怪的做法。